|
) q8 t9 H# E, w8 r+ @ M 
/ ~- ~2 G/ J: N. s6 z 各位同学大家好!我是李永乐老师。
1 ^" m8 { P' c" [- y+ a8 ~ 杨振宁先生出生在1922年10月1日,到今天刚好100岁。他是当今中国乃至世界最首屈一指的物理学泰斗,他的成就可以与爱因斯坦比肩。但是大部分网友熟悉杨先生,还是因为1957年,他和李政道一起提出了“弱相互作用下宇称不守恒”,共同获得了诺贝尔物理学奖。这是中国人第一次获得诺贝尔奖。
( m6 S# D' Z2 [ 
杨振宁和李政道 许多网友问我:这个“弱相互作用下宇称不守恒”到底是啥意思呢?它为什么这么重要呢?为什么说杨振宁是当今最伟大的物理学家呢?在杨振宁先生百年华诞之日,我们再来讲讲这个问题,为杨先生祝寿。
# l3 T% f P: O h2 ^# l7 u+ h7 o 01 对称与守恒
* ~% i( A% S4 O s1 ` 首先,我们要讨论一下物理学中“对称”与“守恒”的关系。
7 R( c1 x1 X/ A5 C+ k 20世纪初,德国著名女性数学家埃米·诺特提出了诺特定理,她说:系统中每个连续的对称性,都会对应着一个守恒量。 8 \- M( S# u: m2 V

诺特定理 比如:物理规律都满足时间平移对称性,意思是说,今天的物理规律和明天的物理规律是完全一样的,物理规律不会随着时间发生变化。根据诺特定理,这种对称性一定对应了物理学中的一个守恒量,这个守恒量就是能量。
+ _9 W4 }" J; t 为什么呢?我们用反证法来证明:假设物理规律会随时间变化,那么能量必定不守恒。 ) _, s6 @; U' q& Y
我们可以这样做:假设万有引力常数会随着时间逐渐地越变越大,那么我就可以在今天消耗能量举起一块石头,明天再让这个石头落下来,释放出能量。因为明天的万有引力常数大了,所以石头下落时,可以释放出更多的能量。这样一来,通过一个循环,我在不引起任何其他变化的情况下,凭空造出了能量,所以能量就不守恒了。根据原命题等价于逆否命题,如果能量守恒,那就必然得出万有引力常数不能随时间变化,这就是时间平移对称性。
) N' u0 v. g$ p# t; F- Y 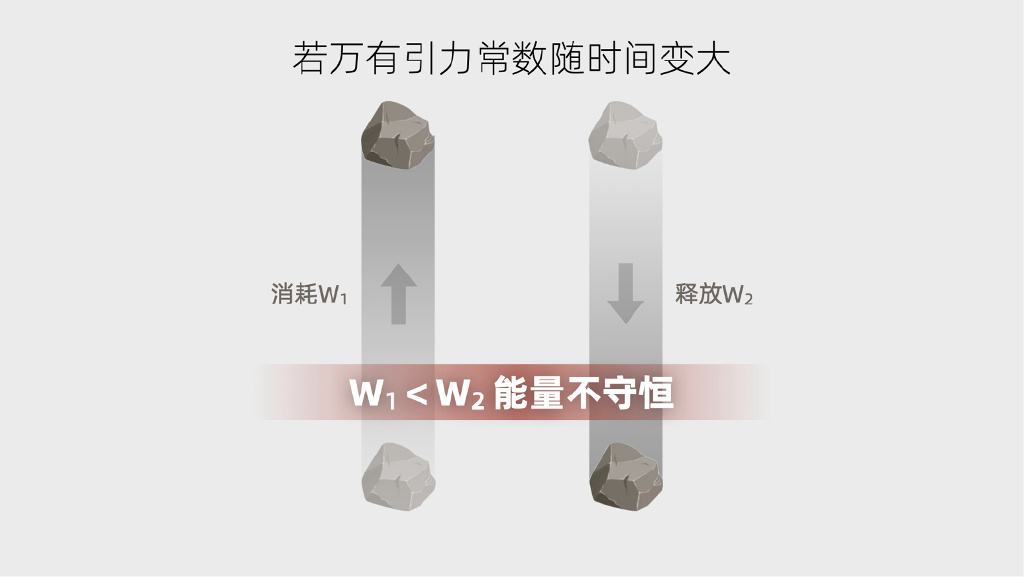
时间平移对称性对应能量守恒 物理规律除了满足时间平移对称性以外,还要满足空间平移对称性——一个物理实验在中国做还是在美国做,得出的规律是一样的。就算拿到火星上去做,结果也是如此。空间平移对称性对应了物理学中的动量守恒。
$ i" O8 _0 G5 M! m, R 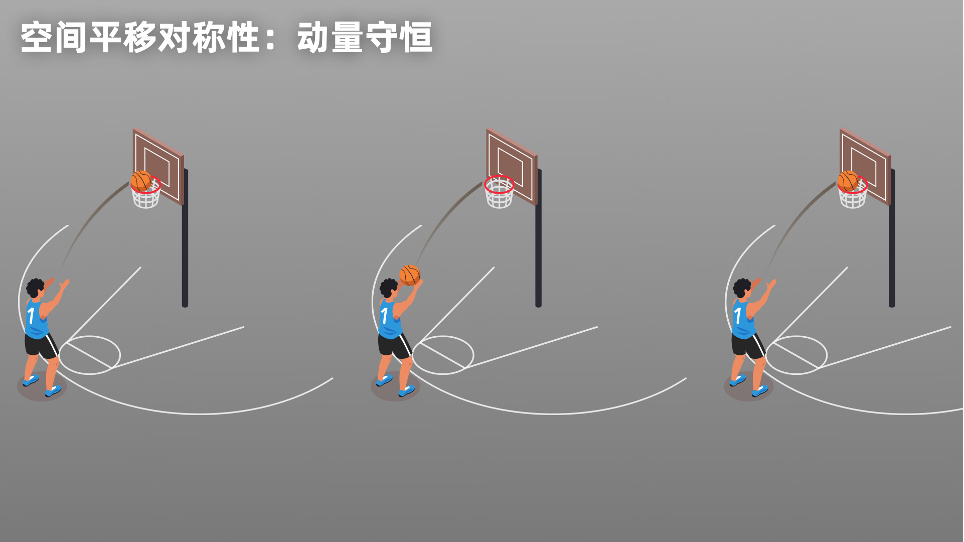
空间平移对称性对应动量守恒 此外,物理规律还要满足空间旋转对称性——向东扔一个篮球,和向南扔一个篮球,得到的物理规律是相同的。空间旋转对称性,对应了物理学中的角动量守恒。
9 H7 m6 r6 v% ^ R 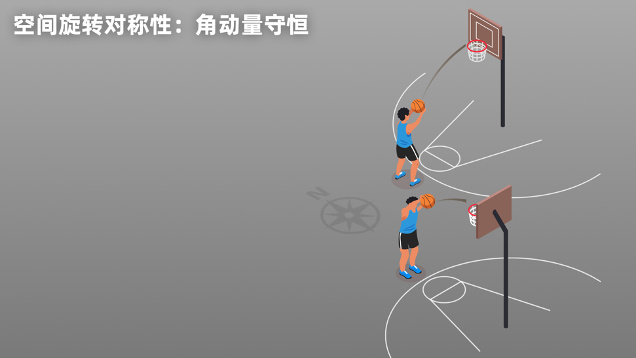
空间旋转对称性对应角动量守恒 最初,诺特认为:对称量应该是连续可微的,也就是可以一点点地改变。比如时间的平移、空间的平移和旋转都是连续可微的。但是后来人们又发现了一种不连续的对称性——镜像对称,物理规律也普遍满足镜像对称。
1 Y' h: \3 A9 B. x 例如:我扔出一个篮球,篮球会经过一条抛物线轨迹。如果在我对面有个镜子,镜子里边的篮球也会经过一个抛物线轨迹。你会发现:不管是镜子外面的世界,还是镜子里面的世界,物理规律也是完全一样的。如果你只看篮球经过了一个抛物线,是没有办法区分这个世界到底是镜中世界还是镜外的世界的,这就是物理规律的镜像对称性。
' {& O8 Q0 N( ^; }4 z/ [ 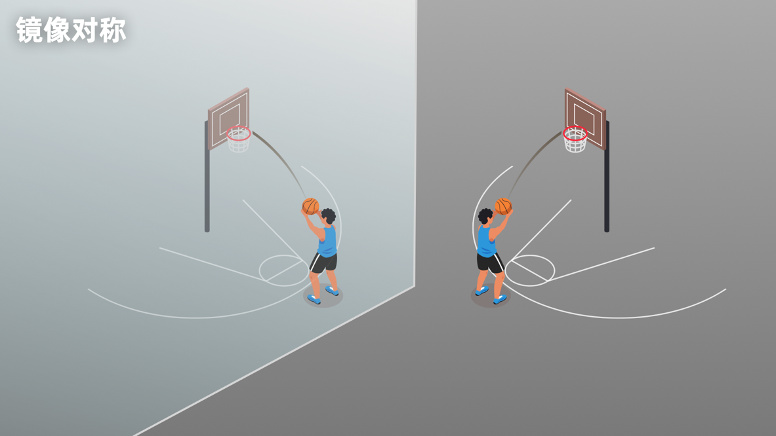
镜像对称 镜像对称又对应了一种什么守恒呢?1927年,美国物理学维格纳提出:物理规律的镜像对称对应了宇称的守恒。
4 ?, I" x5 l. O) l+ ] m 
维格纳 02 宇称
: l% C5 s3 S; `+ e2 F0 h5 | 什么是宇称?这个概念不好理解。但是我们上中学的时候学过奇函数和偶函数吧。 ( D& I1 `; D7 A: m- J( b1 |$ R
函数y=x²是偶函数,因为有它的中央有一条对称轴,如果我们沿着这个轴把函数图像左右翻转一下,你会发现左右两边的函数图像重合了。
+ P7 `! S0 a! V% B 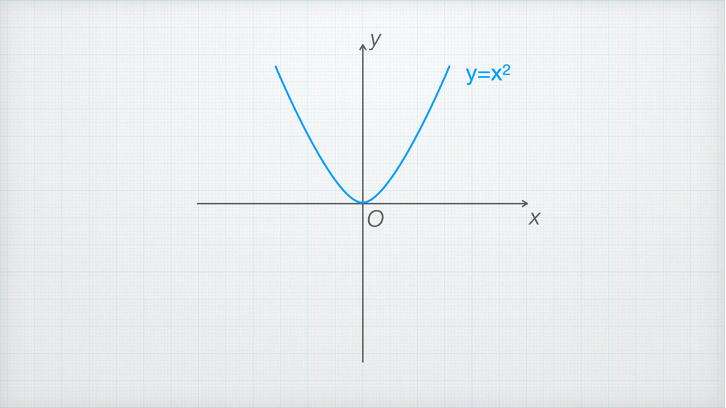
偶函数 而函数y=x³,叫做奇函数,它不存在对称轴,如果我们非要沿着y轴左右翻转一下,你会发现你会发现它的上下颠倒了。
5 i/ B3 p6 l4 i: z+ { 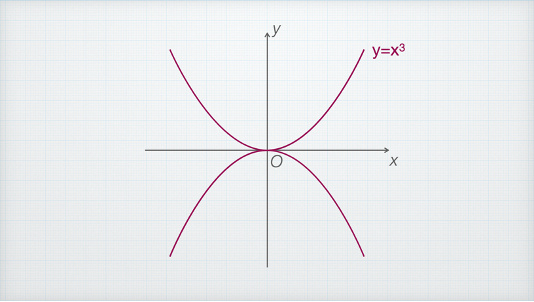
奇函数 我们知道:量子力学中,粒子的位置是不确定的,需要通过一个波函数去描述粒子在不同位置的概率。如果这个波函数是偶函数,我们就叫它偶宇称,如果波函数是奇函数,我们就叫它奇宇称。 . I3 C L; y) d* E t
物理规律的镜像对称性对应了宇辰的守恒,也就是说:如果一个粒子的波函数最初是偶函数,那么它将一直是偶函数;如果它最初是奇函数,那么它将一直是奇函数。 9 @4 t. ~8 @* H( @0 @
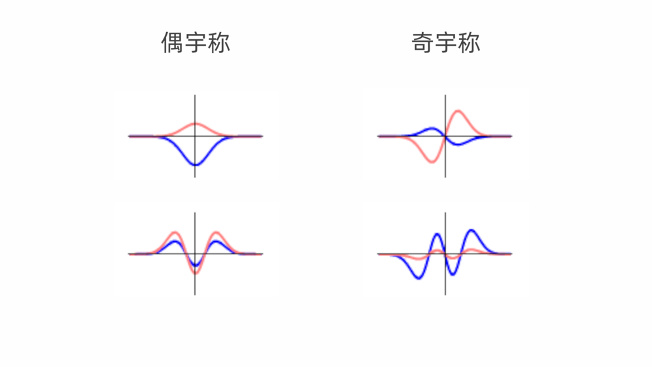
* o p, U9 t0 v5 Y9 ^ 人们曾经认为:宇称守恒就和能量、动量、角动量守恒一样,是一个普遍存在的规律,直到杨振宁和李政道的出现。 / B# o6 I2 i, M& A3 C; `- ~
03 θ-τ之谜
6 Z B2 l7 Z* v 宇称不守恒的故事,要从著名的θ-τ之谜说起。
6 Y2 A K. z' @5 H0 k 有一副很有意思的漫画:粒子物理学家如何研究青蛙的内部结构。粒子物理学家会把一只青蛙放进枪里发射出去,然后撞向另一只青蛙,两只青蛙撞得稀巴烂后,粒子物理学家再去看这些碎片。 ; Q) E( `3 s; c
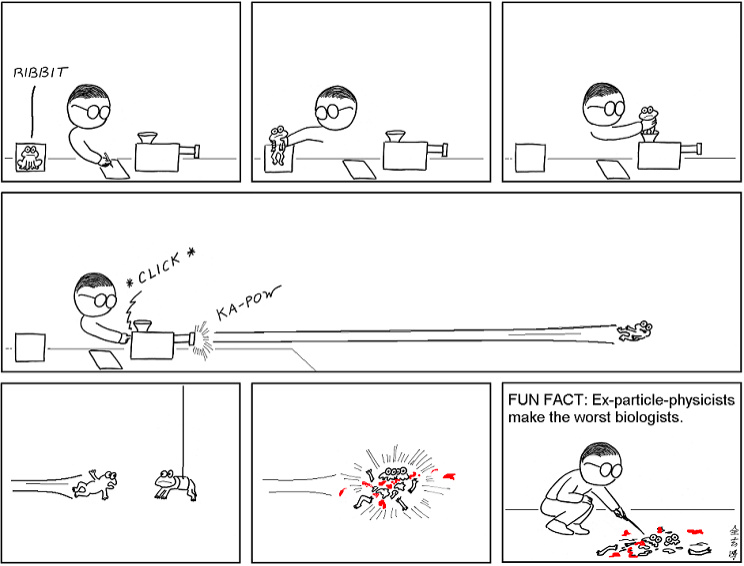
物理学家是如何研究物质结构的 这幅漫画中表现的就是粒子物理学家的日常工作:科学家们首先会造一台加速器,把某种粒子加速,然后让它撞向另一种粒子,撞击之后就会出现许多千奇百怪的碎片。通过这种方法,人们发现了θ粒子和τ粒子。
1 d9 b7 B1 ?' y θ粒子和τ粒子的物理性质非常一致,它们质量相同,电荷也相同,就连寿命也是一样的。那么我们怎么知道它们是两种粒子呢?因为它们的衰变产物不一样。 : f2 a4 {3 _( {/ j0 { i' ~
θ粒子可以衰变成一个π+介子和一个π⁰介子,而τ粒子衰变之后是两个π+介子和一个π-介子。更重要的是:θ粒子衰变产物是偶宇称的,根据宇称守恒,θ粒子也应该是偶宇称的;而τ粒子的衰变产物是奇宇称的,所以τ粒子也应该是奇宇称的。
8 j: y& H H4 t- f6 V* e. `4 Q" C 
6 k }" i$ @6 C+ P. H 所以,科学家们断定:尽管θ粒子和τ粒子看起来非常相似,但是它们宇称不同,一定是不同的粒子。可是话又说回来,为什么两个不同的粒子会具有几乎相同的性质,却唯独宇称不同呢?这就称之为θ-τ之谜。在二十世纪五十年代,这个问题被认为是粒子物理的关键问题之一。 ; K. `5 s& c* Z1 Q: z) Y
04 宇称不守恒
1 [+ x2 I! J, G3 Q! y+ |1 O, x. U 针对θ-τ之谜,顶尖物理学家们提出了很多种理论,但是最终解决这个谜团的是杨振宁和李政道。在1956年的一天,他们两人在一次就餐时迸发出一个想法:也许θ粒子和τ粒子本身就是同一种粒子,只是它们衰变时,宇称发生了变化! : D" m" l5 C: G! [0 q4 W

杨振宁和李政道 中学时我们就学过,自然界有四种基本的相互作用: 1 U- ]- t1 N: n h. Y P d
第一种叫电磁相互作用,比如两个电荷之间作用就是电磁相互作用。
3 U# p! d7 I& x 第二种叫万有引力,比如太阳和地球之间的力就是万有引力。
* i, Z @8 M! S$ Q( Q J3 ^6 W1 h4 C 第三种叫做强相互作用,强力能够把质子束缚在原子核里。 ) {& E. `1 P3 L2 r
第四种力叫做弱相互作用,在θ粒子和τ粒子衰变的过程中,就是弱力在发挥作用。 3 Z( a1 ~1 S+ b/ y6 S3 G" N& h/ @
 0 Z5 g" a1 y/ Y& c- E
在前三种相互作用中,都有切实的实验和理论支持宇称守恒,但是在弱相互作用下宇称到底是不是守恒的,还没有实验或者理论的证实。于是,杨振宁和李政道两个年轻人大胆的猜测:也许在弱相互作用下,宇称就是不守恒的?所以同一种粒子,有时候通过弱相互作用衰变成偶宇称的粒子,有时候通过弱相互作用衰变成奇宇称的粒子。如果真的是这样,θ-τ之谜就被解开了。 6 r0 d! _% j, h4 w) ^" A9 ~4 E
不过,对称性是宇宙的基本的规律,在杨和李之前,所有的物理规律都是建立在对称性的基础之上,就连爱因斯坦的相对论也不例外。两个年轻人说物理规律是不对称的,这很难让人相信。 4 U7 {2 M% c- A
于是,杨振宁和李政道决心,要通过实验验证自己的猜想。 - S7 n3 }+ t! h
05 吴健雄实验
" J0 O! n/ p9 t 1956年底,杨振宁和李政道找到了正准备利用假期出去度假的华裔女物理学家吴健雄。吴健雄是一位非常杰出的女性,她后来成为了美国物理学会会长,被称为东方居里夫人。
# Y" L, ~) m2 W$ B; ^ 
吴健雄 杨振宁和李政道对她说:我们设计了一个实验来验证弱相互作用下宇称不守恒,您能不能帮我们把实验做出来? : Z6 F2 ^. J- k) s* Y1 U/ O0 m
具体的实验过程是这样的:
1 L$ w Z0 M& L 钴60是一种放射性元素,在弱相互作用下可以衰变成镍、电子、反电中微子和两个光子: 7 r$ |$ T: V) G) J1 g L/ x
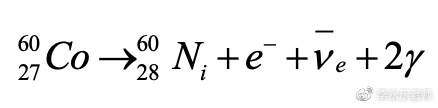
; D% h5 Z. M2 a. x3 d: ~ 我们要关注的是两个物理量:钴60原子核的自旋方向和电子的发射方向。通过外加不同的磁场,可以人为控制两个钴60原子核的自旋方向相反,这样它们刚好是镜像对称的,我们可以称其中一个钴60为“真实世界”,另一个自旋相反的钴60为“镜像世界”。
: W2 K# B3 O4 F' F. x, `! [* s 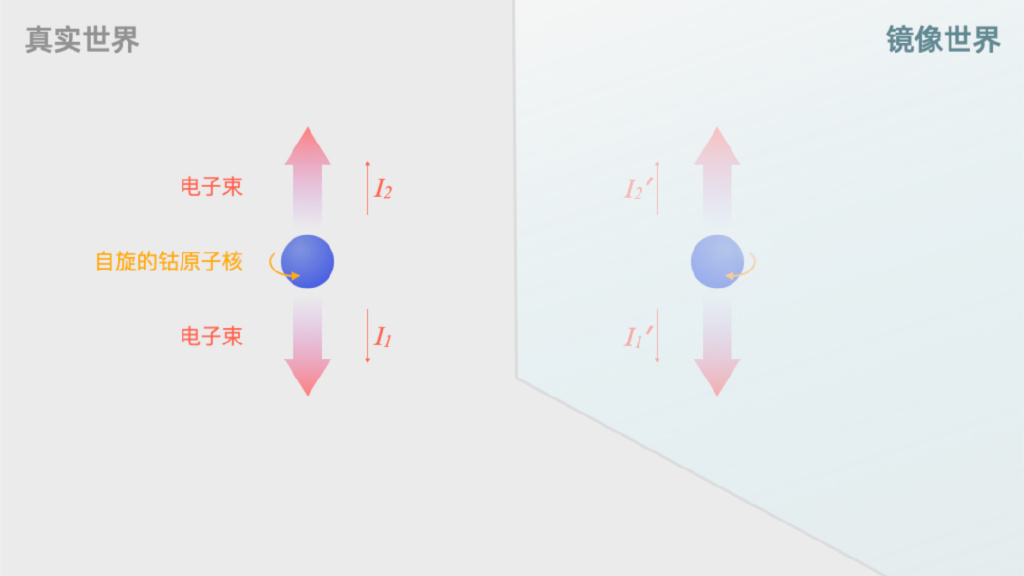
( G5 ], i! k, V; A. P& O* V 因为衰变,无论是“真实世界”的钴60,还是镜像世界的钴60,都会向外发射电子。这些电子要满足什么规律呢?
) q: W* p" f. P9 [, @ 首先:根据已经证实的空间旋转对称性,真实世界只要旋转1800就能变成镜像世界,因此真实世界中向上发射的电子束,一定和镜像世界向下发射的电子束强度相同;真实世界向下发射的电子束,也一定和镜像世界向上发射的电子束相同。也就是 I₂=I₁′,I₁=I₂′。
. P4 y7 o6 [8 [* A9 ~ 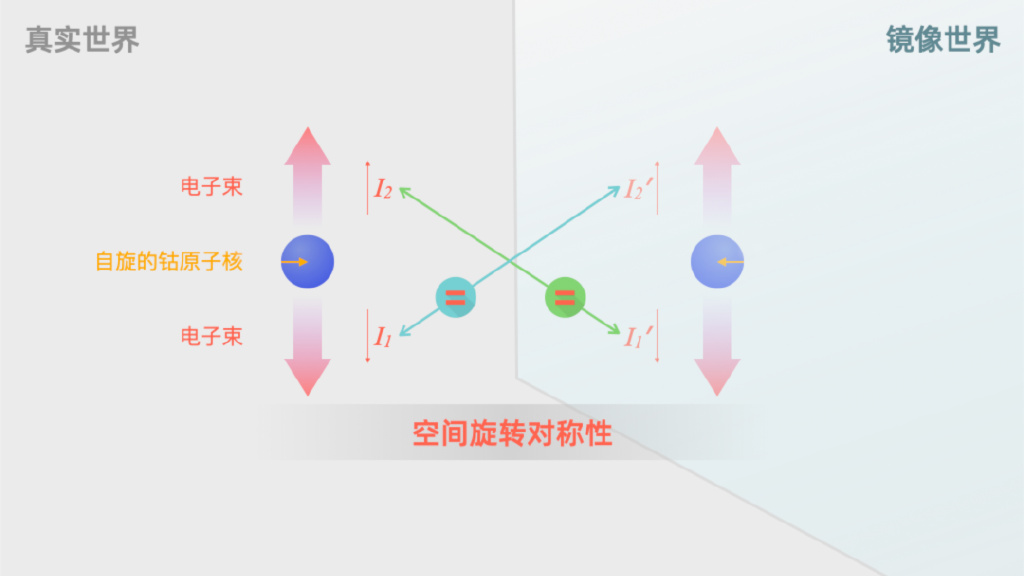 $ `0 o* m, s& ^. X3 G5 C3 p
与此同时,如果宇称也是守恒的,那么根据镜像对称性,真实世界向上发射的电子束和镜像世界向上发射的电子束强度一定相同,真实世界向下发射的电子束和镜像世界向下发射的电子束强度也应该相同。也就是 I₁=I₁′,I₂=I₂′。
' J& r) s5 E+ C0 d% S# L+ j 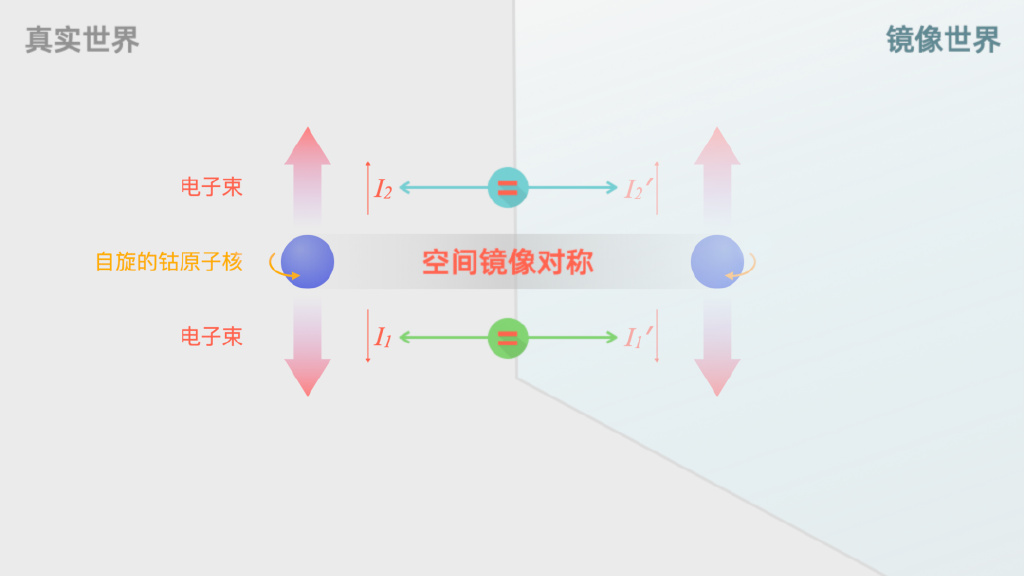
8 N7 d+ D3 R/ s8 C! V3 Q- T 那么,根据以上两条对称性,自然就有四个方向的电子束强度都相同,即I₁=I₂=I₁′=I₂′。
$ x, i" f% p7 v. _! j+ k# g Q 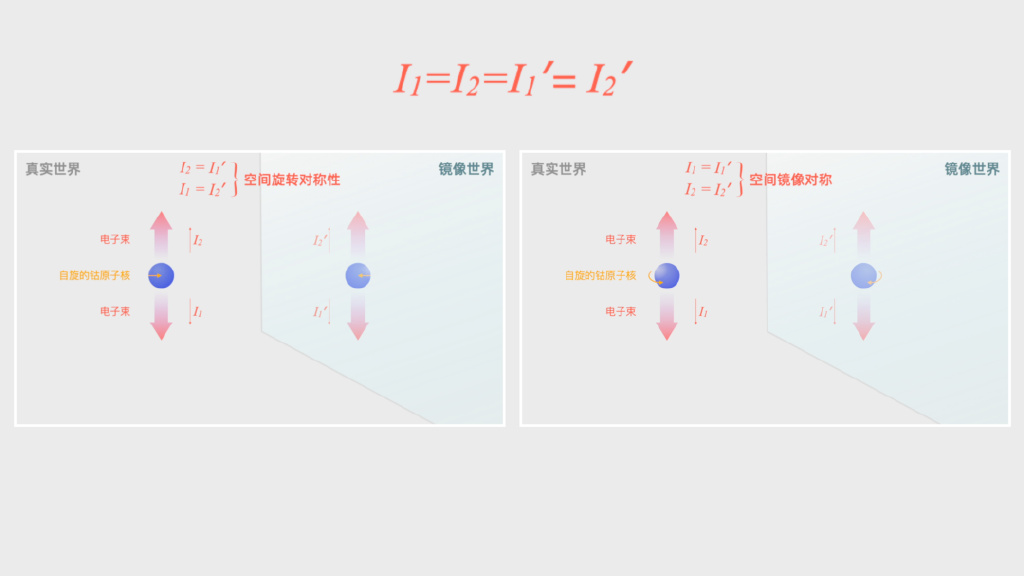
. a/ i; K" l! T( {" m5 ]/ g 但是,假如杨振宁和李政道的猜想是正确的,在弱相互作用下宇称不守恒,那就会出现钴60向上和向下发射的电子束强度不同的情况,实验就是要找到这种不同。
7 t) d0 K1 C( X; w, j( F" N2 z! p$ m 听上去不难,但是实际做起来,难度还是很大。因为原子核都是在不停的运动的,它怎么会听话的排成整齐的镜像呢?方法就是降低温度,只有温度降到足够低,原子核的运动才能被束缚住。 $ s) j6 t) [4 ?% ~8 V$ p$ V
吴健雄被这个新颖的想法吸引了,她取消了自己的休假,在美国国家标准低温实验室里完成了这个实验。她把钴60的温度降低到0.003K,这已经非常接近绝对零度了,再通过磁场控制钴核的自旋方向,然后统计了大量钴60的衰变结果,发现了一个惊人的事实:
! o& y( W' {1 d' n& H9 d 在实验中,钴60向上和向下发射的电子束强度不同! & s! x u5 \% O
真实世界的里的钴核向下发射的电子多,镜中世界里的钴核向上发射的电子多,每一个钴核自旋方向和电子发射的优势方向都满足左手定则!就好像它们都是左撇子一样!
) A6 z; J& n( I* P& T' y 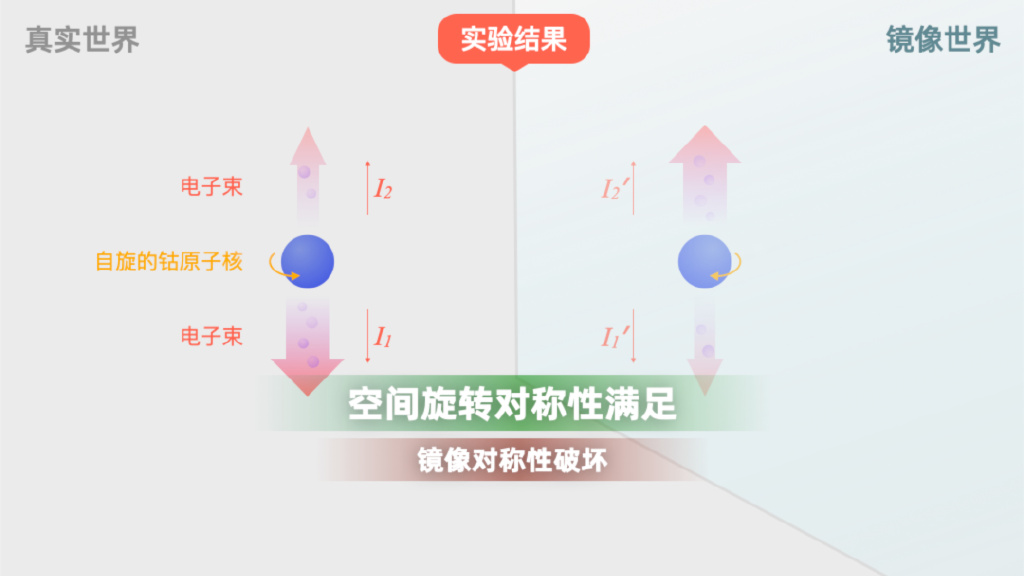 4 @% l* \# {; w( j" s1 x
你看,如果把真实世界的钴60原子旋转180度,就能变换到镜中世界,所以空间旋转对称性还是没错的。但是,如果把真实世界的钴60做一个镜像,就和镜中世界完全不一样,所以在弱相互作用下,镜像对称性被破坏了!宇称果然不守恒了! - f! F6 `8 M# t( M
1957年初,吴健雄发表了自己的实验结果,支持了杨和李的结论。尽管如此,还是有许多顶级物理学家不能接受。比如:被称为“物理学界的良心”的泡利说:我不相信上帝是左撇子。理查德.费曼说:我赌50美元这个实验肯定是做错了。布洛赫更是夸张的说:如果宇称不守恒,我就把自己的帽子吃掉。
+ m7 A: L& ?& e 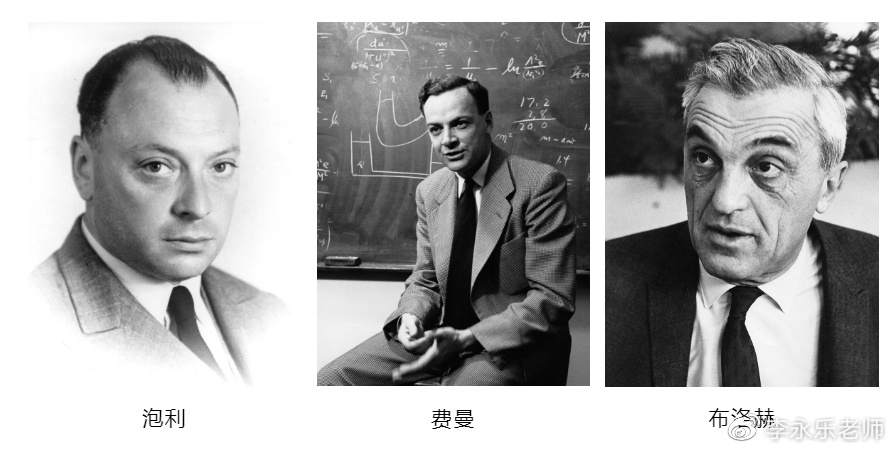 9 a' Y3 b6 Y9 l0 {. v3 Z
尽管有许多人反对,但是实验结果是无法反驳的。1957年,诺贝尔物理学奖授予给杨振宁和李政道,那一年杨振宁35岁,李政道31岁。想想爱因斯坦从1905年提出光电效应,到1921年获得诺贝尔奖,中间相隔16年。杨振宁先生和李政道先生从提出理论到获奖,中间只隔了1年。 0 M9 u8 ?* }0 \7 ^

' W- [0 ?0 k, Q4 y, J 宇称不守恒是一个非常重要的物理结果,它打破了人们的固有观念,把对称性撕开了一个口子。人们发现:在某些情况下,对称性是有破缺的。正是因为对称性的破缺,一种统一的作用力,才慢慢变成弱相互作用和电磁相互作用。反过来,我们也可以用一种理论解释弱力和电磁力,这就是弱电统一理论。
( ]' w: {2 P% J7 \7 b, f* k 其实,早在1954年,杨振宁和米尔斯就写下了杨-米尔斯方程,但是直到人们理解了对称性破缺,才知道了这个方程的重要性。再后来,温伯格提出了弱电统一理论,盖尔曼等人建立了描述强相互作用的量子色动力学,这一切构成了我们今天对围观世界的最深刻认识:粒子物理的标准模型。 % m9 W# n! q2 _$ @

杨振宁和米尔斯
温伯格
盖尔曼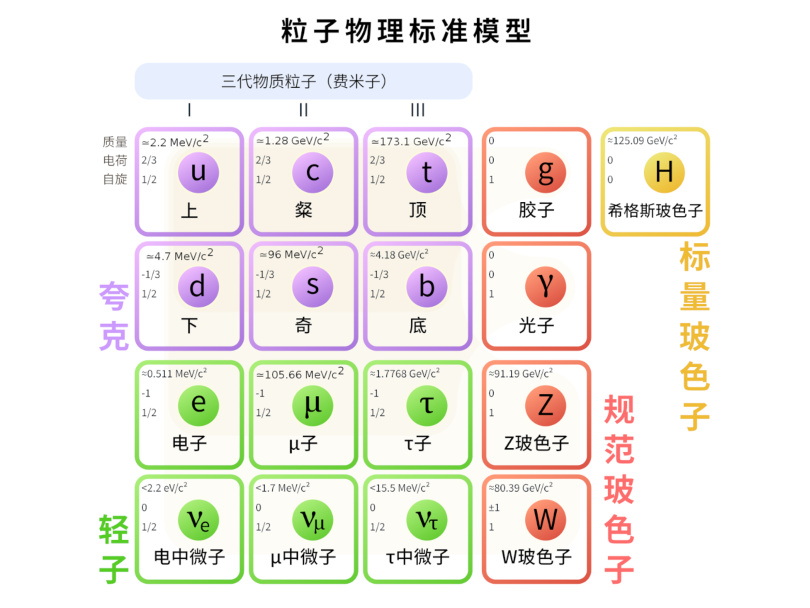
粒子物理标准模型 二十世纪上半叶是一个年轻物理学家辈出的时代,保罗·狄拉克提出狄拉克方程的时候26岁,海森堡提出不确定性原理的时候也是26岁,爱因斯坦提出相对论和光电效应方程的时候25岁,也许正是因为这些年轻人没有太多条条框框的束缚,才能够为物理学做出突破性的贡献。
* A; m5 g: n% f 
) i6 A& {5 u4 Z3 f$ L1 h/ N 在杨振宁先生提出宇称不守恒和杨-米尔斯方程时,都受到过当时的物理学大家的猛烈批评,可是杨先生在压力下依然坚持了自己的想法,才有了震惊世界的发现,成了物理学泰斗。回想起爱因斯坦提出的相对论和光电效应理论,不也是如此吗?
* m! @2 \# o% P! t1 s 感谢大家观看本期内容。让我们一起祝杨先生生日快乐! 6 m: @; P$ x w5 x$ v$ }9 Q
0 [$ O3 W$ D, C O2 ]6 y7 D1 _) Q+ X
7 d: M8 N$ e! l9 o4 _; t6 G
2 \4 Z* x5 x( f
6 e! {# W: P0 p! c- ^ ~8 t* [9 P+ e( Y# c2 L5 i
) ]) s. N" w3 A8 a2 p8 k$ e" x: y: p$ ?0 f* c, J3 X5 z. v
$ D- I, s' v0 f" C' P& m
3 w: C+ p8 x0 G; c) b4 a: j: d+ Z& u) i8 N8 Z9 }+ z
| 

