|
! z2 d" y( D G8 M
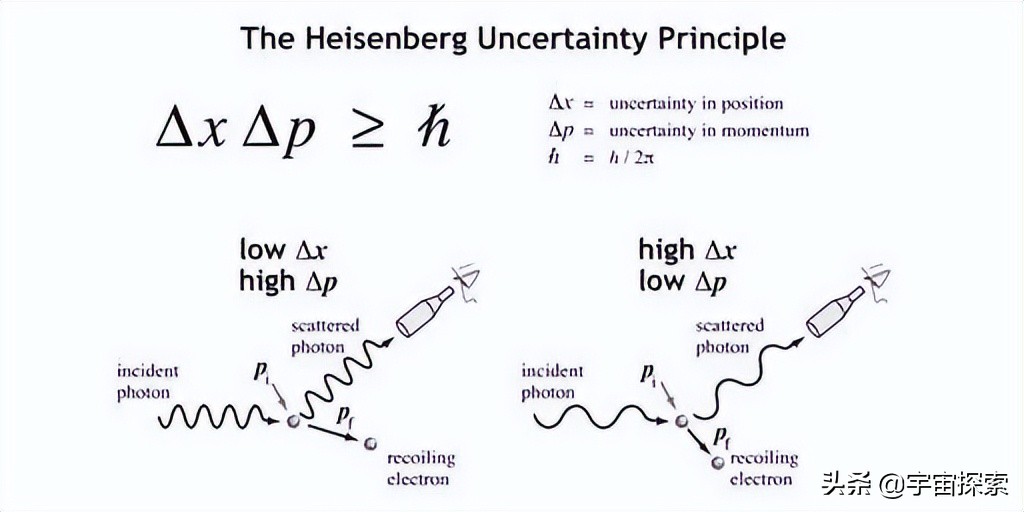
海森堡的测不准原理,与测量方法没有关系,也不是测量仪器精确与否的问题,而是大自然的内在秉性决定的,表现出来的是一种大自然法则。 5 s9 M( ?$ b( G- |8 K1 Z
 , W3 s: u% T3 E$ B! k
量子力学发展了一百多年了,如今我们知道“测不准原理”的说法并不严谨,应该叫“不确定性原理”才更严谨,不然的话真的容易让人产生误解。
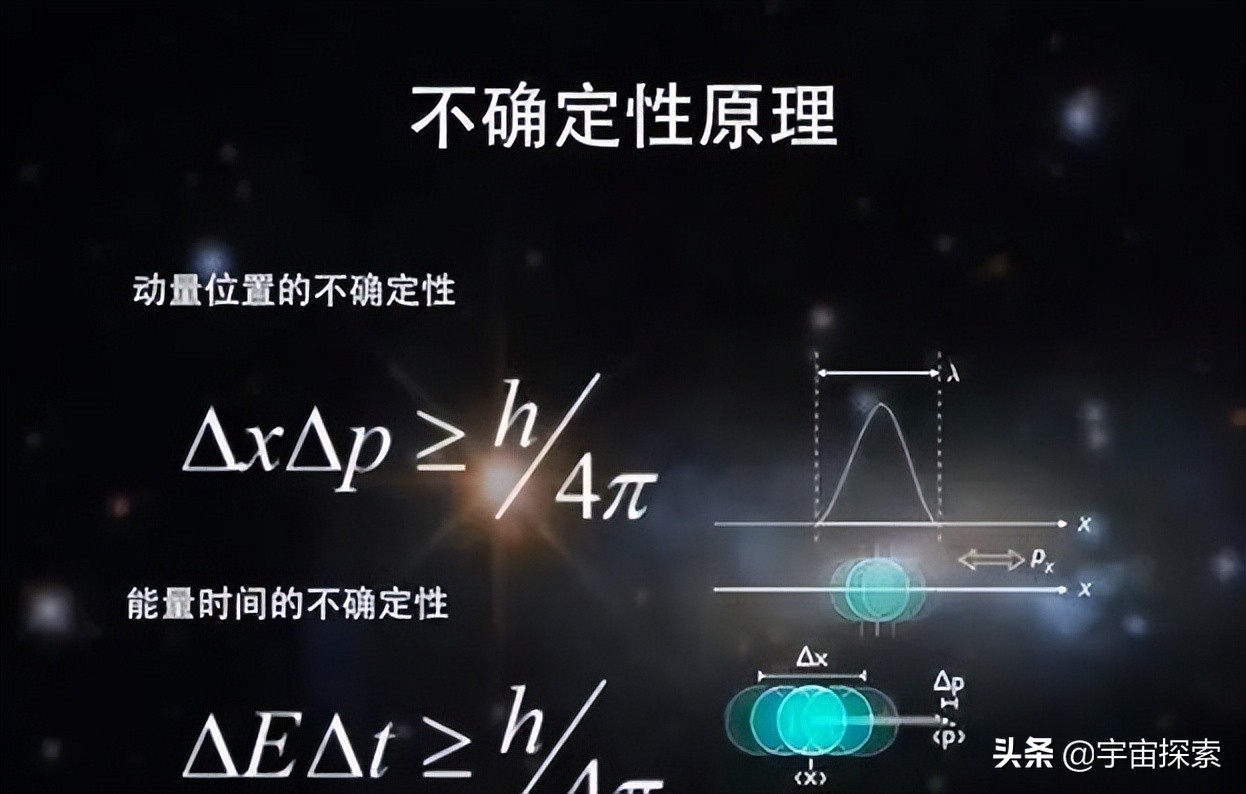
1 w; U( Y' g/ t* ^) S 不确定性原理,只要弄懂一个公式,就能很好理解了。这个公式就是:ΔxΔp≥h/4π / Z$ `" B( W2 O3 l8 Z
公式并不复杂,很容易理解,其中Δx表示位置的变化量,Δp表示动量(速度)的变化量,h表示普朗克常数,π是圆周率。
) N6 B v' ]) J9 u! e, G 公式的含义是这样的:微观粒子的位置和动量(速度)无法同时确定,粒子的位置越确定,速度就越不确定。相反,速度越确定,位置就越不确定。 9 Q! Z# l1 W6 Q P
普朗克常数h非常小,只有6.62607015×10^(-34) J·s。而由于在宏观世界里,Δx与Δp都非常大,所以,不管在什么情况下,上面的公式都成立。 ' G/ t1 |; I$ r1 J% b
但在微观世界就不一样的,Δx与Δp会非常小,这样一来,两者之间就会彼此限制了。
) w7 R" W% @9 l9 u 举个例子,如果Δx非常小(也就是位置比较确定),那么Δp就必须足够大才行,才能使得公式成立,Δp足够大意味着位置速度不确定。反之亦然。 0 J7 B6 n0 n- ]6 i/ Y" `# Y
从公式中可以看出,这种不确定性与观测方法没有任何关系。 * f: V4 T; M& f/ l& v
除了位置与速度有这种不确定性关系,能量和时间同样有这种关系,用公式表示就是ΔEΔt≥h/4π。 7 k4 v3 P' B0 A% c
 + s/ {+ [8 ?: d3 t2 @ ]
两个公式表示的含义是一样的,只需要把位置和速度替换成能量和时间就可以了。
* m' A2 Q( N( u% H3 ? 能量和时间的这种不确定性关系,可以很容易地推导出来量子世界里的“量子隧穿效应”和“量子涨落”。
2 t, H, d, V) h2 q 比如说,当Δt非常小时,意味着ΔE可以变得非常大。这也是为什么微观粒子可以瞬间越过“能量势垒”。在现实世界举例子,比如说你最多只能跳过2米高的墙,那么“2米”就是你的能量势垒,你不可能跳过超过2米的墙。
6 y9 u: [+ a8 {0 H8 m* H5 W/ n 但按照量子力学的不确定性,只要你的Δt足够小,你可以在某个瞬间跳过10高的墙!是不是有点不可思议?
) M/ b, t! u, o9 G; k* j$ m, P 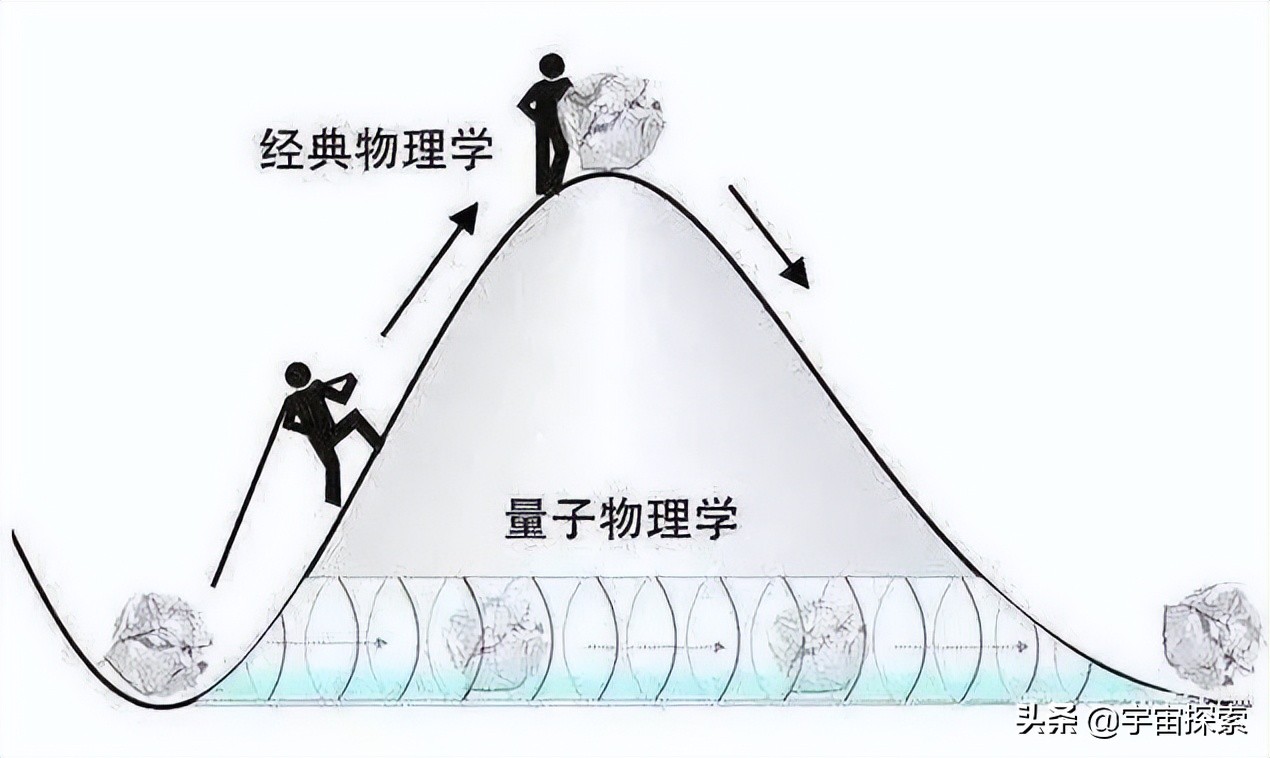 9 G1 c5 V. Q# E, T
还有,我们在现实世界中想翻越一座山,必须从山脚跑到山顶,然后再到达山脚。但在量子世界,就不需要如此麻烦了,只需要在Δt内到达另一端的山脚就行了,这样你就可以先“赊借”能量,然后瞬间归还能量。 ! B! h3 c2 m( `! H l8 o3 g8 B! ^3 G
但是在宏观世界,上述情况很难出现,因为我们本身的质量太大了,还有要求Δt足够小,这两点都限制了我们进行“量子隧穿”。
9 R6 l" m$ R* S* D# s2 @ 还有就是量子世界里的量子涨落。在极短的时间里(Δt足够小),就可以凭借赊借真空的能量衍生出虚粒子对,然后瞬间相互湮灭,把能量归还给真空。只要Δt足够小,大自然一点也不反对这样做,而且这种情况必须上演。
1 D! j @$ {% d y! a1 y' {0 ` 这就有点类似现实世界的“有借有还,再借不难”,而且借钱还钱的时间必须要尽可能短,这有这样才能一直“向真空借钱”(借能量)。
! I( o0 _" J9 J& R1 A3 S* E# l! F. W q {% a
3 ^9 f1 R; d" ^6 ^. s ?
a n3 c" t; T0 L
$ B; ^/ x) C1 z p$ s# g9 F
5 [' P1 }* k3 I( R& [! C9 a6 a, \
6 @, @( k3 j8 F) s
% z' `7 X# o' x' {+ g: U
, j$ W. I. Q( f3 x
2 H$ ~' B$ d' K2 k, e2 v1 e
+ J7 h& U5 L7 {% x C |