|
3 }: s( V& H& p
原标题:弹性模量的物理学本质
+ e/ F7 F: n& ]) [1 `; q( Z6 c( A+ {! Z/ R7 r' z
从宏观上讲,弹性模量表征了材料在一定的应力作用下发生弹性变形的难以程度,弹性模量越大发生变形越难。从原子间相互作用力角度来看,弹性模量则表征了原子间结合力强弱的程度,弹性模量越大,意味着原子间结合力也越大。
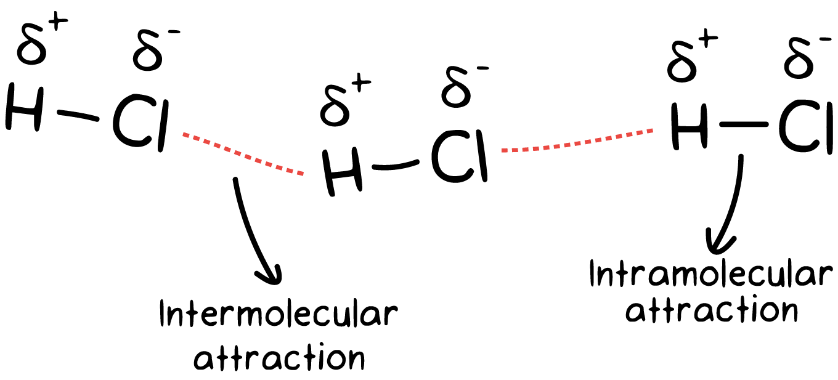
, S- e: v8 K$ ], B, Z 如由分子组成的材料,原子先通过分子内结合力(如离子键、共价键)组成分子,分子再通过分子间结合力(如极性共价键)组合成物质。通常情况下,分子间的结合力要比分子内结合力小的多。材料在发生弹性变形时,可认为是分子间距被拉大/压缩,分子间结合力随之改变所产生的结果。 0 ]5 i! [# M! z# G: J1 |6 e
/ _6 I' k, p# W5 U- }/ ]# t
图1 分子内和分子间作用力 来源:网络
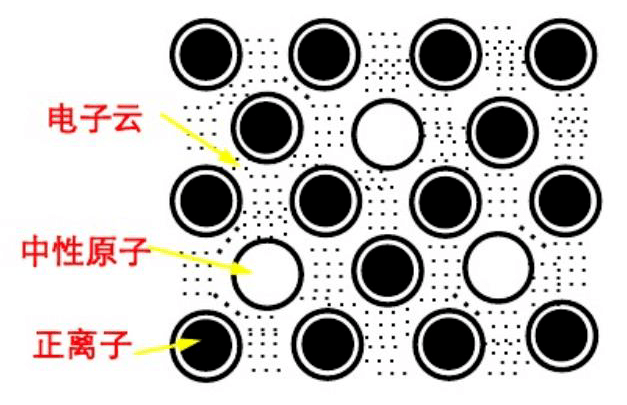
" J8 f! B! D% J$ c7 C 对于金属原子,由于其最外层因与原子核的结合力较弱,很容易脱离原子核的束缚而变成自由电子。当一群金属原子聚集时,所有金属原子的最外层电子、甚至是次外层电子都有可能脱离原子核的束缚,变成自由电子,这些电子为所有的原子所共有,形成电子云。失去电子的原子变成离子,而离子就沉浸在电子云中。金属离子与公有化电子的静电作用结合而成金属键,形成金属材料。 8 a2 _+ p; V }' g
. M, ]- F) r# x& T) D
图2 金属材料微观结构示意图来源:网络
E* I) Z) L( H4 i/ C! k* A 从微观粒子的结合强度来看,金属键等价于分子内作用力,其结合强度要远高于分子间结合力(如极性共价键),因此金属材料(如钢)相比于分子材料(如塑料)更难以发生弹性变形。
+ ]" U6 W) n- Z) |8 g: S 我们可通过图3所示为双原子受力模型来理解原子间的结合力。当双原子被压缩时,原子之间将产生抵抗压缩的排斥力,双原子被拉伸时,将产生抵抗拉伸的吸引力。一般认为,原子间的引力是正离子(失去电子的原子核)和自由电子之间的库伦引力产生的,斥力是由正离子和正离子、电子和电子之间的斥力产生的。 8 B! {. _. i q4 T1 K/ f
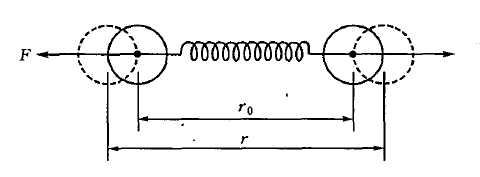
, |2 I2 S. a% V, q 图3 双原子模型 [1]
/ l- @$ h" R) A. [) y5 s+ }9 G 画出引力、斥力示意图,如图4所示,其中N 1 和 N 2 表示两个原子,r表示它们的间距,其中曲线1表示引力随两者间距的变化规律,曲线2表示斥力的变化规律,曲线3表示引力和斥力的合力变化规律(叠加曲线1和2);作用能图给出了两原子形成的作用能(势能)随原子间距的变化规律。可见,当双原子处于平衡位置时,势能最低,两原子最稳定,当原子被拉开或压缩时,能量增加,一旦撤去外力,原子就要回到能量最小的平衡状态,这一过程就是弹性变形的过程,又是最小作用量原理的一个例子。 / k0 F% R# k3 }0 {
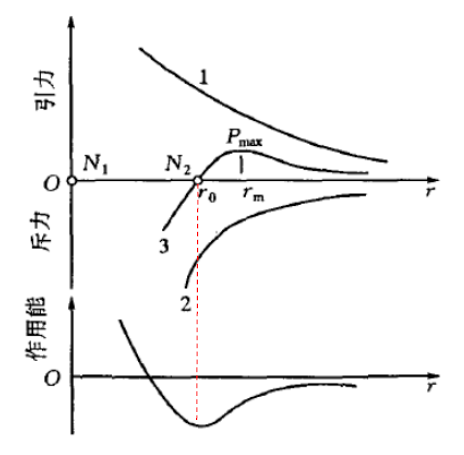
/ ~" k7 n7 W% {, ~1 k 图4 原子间引力、斥力,及作用能示意图 [1]
$ ?* V) x" S; x8 I3 S 由于弹性模量是原子间结合力的反映,影响原子间结合力的因素都会影响弹性模量。例如,熔点与原子间结合力有关,熔点高意味着原子间结合力强,所以一般情况下熔点高的材料弹性模量也越大;另外,环境温度升高,会增大原子间距,从而导致结合力变弱。因此高温下,弹性模量也会降低,如烧红的铁更容易被锻造。
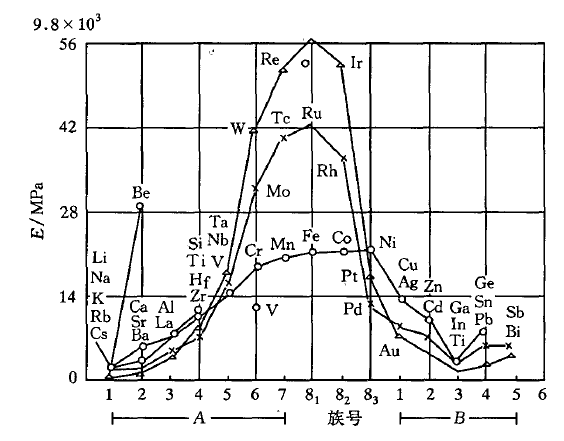
+ V6 R% G& A! T( @ 人们还发现弹性模量还随原子序数呈周期变化,同一周期元素,如Na, Mg,Al, Si等,弹性模量随原子序数增大而增大,这与元素价电子增多及原子半径减小有关。同族元素,如Be, Mg,Ca, Sr,Ba等,弹性模量随原子序数增大而减小,这与原子半径增大有关。但对于过渡金属来说,由于它们的d层电子未被填满而使得原子间结合力增大,致使如Fe,Ni, Mo,Mn等金属的弹性模量都很大。 u4 ]* W( s8 [/ f E
9 F3 m+ u& Z, m5 m
图5 弹性模量随原子序数的周期性变化 [1] 1 E v# x2 H/ f# M
此外,还有一些其它与材料性能相关现象。例如人们观察到铁磁性材料在磁饱和状态下比未磁化状态下的弹性模量要高,这一现象称为弹性的铁磁性反常,是由磁致伸缩引起的。另外,人们也观察到Nb-Ti合金材料在超导转变状态时也伴随着弹性模量的突变,但其发生机理还需要进一步研究。
1 j; N: u2 E1 z! }' f5 Y) B 上世纪20年代(1920s)开始,人们借助于经典力学的基本原理,通过经验和半经验参数来计算分子结构和能量,称为分子力学(也称力场方法)。分子力学将分子或原子看作是由一组靠弹性力(或谐振力)维系在一起的集合,以键长(相当于原子间距)和键角(三个原子组成的角度)来描述分子构象,而真实的分子构象要满足分子总能量取最小值(最小势能原理),以此来求解分子的真实构象。以Etotal(这里E为能量,注意与弹性模量区分)来表示分子总能量,它由以下几个部分组成 2 C3 a: O' N0 e) i

4 Z: }9 t8 v5 a) ^' J 上述每一能量项均由一定势能函数形式和力场参数构成,这样就将体系能量仅作为原子(核)坐标的函数而加以求解,可求得材料的静态结构(分子构象)和各种性能(包括力学、电、磁、热等多种性能)。以分子力学特定的力场为前提,通过运用力、速度和位置等参数动态模拟材料结构和性能的方法被称为分子动力学,也是当前材料科学研究的热门方法。
J/ G r5 F0 F, q1 l/ W, F 近年来,人们又结合第一性原理获得力场参数,即只从普朗克常量、电子的静止质量、电量等三个常数出发,通过求解薛定谔方程获得力场参数,完善了分子力学理论体系。这一理论在当代计算机软、硬件的技术支持下,可实现大体系原子或分子的构象计算,以及材料力学性能的模拟分析。其中优秀的软件如美国Accelrys公司开发的Materials Studio (MS) 软件,以及开源软件包Abinit等。这些软件不仅可以模拟出材料某一方向上的弹性模量E,还可以在三维条件下,模拟材料本构关系的系数矩阵。
; ?4 w4 Y! m# ^% X& p7 r 考虑最复杂的极端各向异性材料,其本构关系可表示为: ; ~1 X1 B1 v1 R7 K/ F: Y O0 v
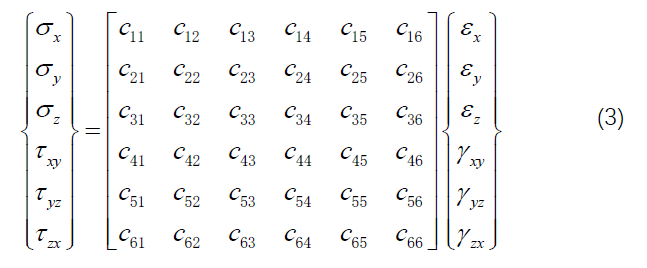
! W% b; z# r8 n) Y6 O, ~$ M
左边为应力分量组成的列向量,可表示某一点的应力状态;右边应变组成的列向量,可表示对应于应力状态的应变状态。中间的C矩阵即为弹性系数矩阵。 , ^- _3 Q6 H* X* z: A3 j
利用分子动力学求得体系(微观尺度的材料)的平衡运动轨迹,可对其进行单轴拉伸、纯剪切形变等操作,然后在原子水平上由位力公式求得某点的应力张量如下 2 K% D- _3 u) L+ C

% g$ u- s* @: O2 A( a" ?) `: e 可见,从物理本质上看,材料的力学性能取决于组成材料的原子的电子结构,更强烈的依赖于其原子和分子的排列方式。因此,利用第一性原理(涉及量子力学)获得力场参数后,将其应用于分子力学或分子动力学,可对材料微观构象进行计算,确定出材料的微观构象,再通过宏观力学的方法,对原子体系(模拟材料)进行力学上的拉伸、剪切等加载模拟,可获得材料的各项力学性能指标(包括弹性模量)。 : D! L0 ^5 ?3 E& u
这就突破了弹性模量等表征材料力学性能的参数只能通过实验测定的局限,它们也可以通过严谨的理论体系进行求解。据文献介绍,从第一性原理出发模拟出的弹性模量与实验测试结果具有较高的一致性,但对于其它参数,如屈服极限、强度极限等模拟还存在较大的不足。但作为一种理论方法,在材料设计、力学性能分析、材料本构关系等多个方面,该方法都具有较大的诱惑力!
! z: ^3 P1 ?, V h! W 声明:公众号偶尔转载的文章出于非商业性的教育和科研目的供大家参考和探讨,并不意味着支持其观点或证实其内容的真实性。版权归原作者所有,如转载稿涉及版权等问题,请立即联系我们删除。
, [: k z$ N* I. z 网站平台:www.posongbi.com返回搜狐,查看更多
( x( m9 i Z/ g- Y7 ], F7 W" J
2 R, G6 q7 U0 e. [) y1 e6 }# G7 c0 P3 T
% d+ c1 |! }" T( K4 X
弹性力学的研究内容及发展概况$ c/ U4 l5 f k. z" i+ M K8 _3 X9 }
% T: [) g2 w+ k% V2 z
( \3 F) G& o l! b" W9 S& ^. O
谈弹塑性力学的物性方程:理论与实验终于协调了
* g2 Y" g4 S# Z; O
. Q3 B! g3 s8 u5 n3 ? k0 P+ z3 E" R+ e% k% k
理论力学、材料力学与结构力学的关系1 ?% @- w; M, y; J3 _4 ~+ o
2 a" Y# Y- f- W" O: [
# ?0 y6 J$ D, a 一名优秀的工程师首先是力学家
8 c. w; h; l$ x5 [" K
8 h8 y0 s6 n" c5 U' H) b( |# L |% r) T B+ ?) T
直观的力学性能-动图讲解
& U6 A& C! ?9 [) s2 _4 g7 H! ^6 x+ a" D% [7 a& c; \
- j) \; X/ \2 H" Q
浅谈有限元方法的核心思想:数值近似和离散化* x9 N& R3 h p* S+ d3 l- o6 q
7 b& n% [0 | N( E1 H' S
) s" B X5 n1 [2 d' ] 有限元四面体网格与六面体网格的争议
) m. M7 k) M' L/ M
' ]; m7 E6 T4 t6 n" b3 x/ v8 u4 r7 f9 O1 Q. X- o/ m& ^; ^3 N& C0 q0 m
关于疲劳问题的有限元分析清单! s' a8 q: [* e( J. i0 l
w( r1 [5 E; g& {% G+ j! r( e5 Q& v; q: }% X( i |" h
如何看“力学”$ m- Q9 ]2 J' b( E$ j
8 I" ^- k5 J; N3 X# B
) t. T% f/ U: q3 n6 m
疲劳失效和SN曲线( o+ Q8 E, [! x6 i" L5 q
, c0 X4 N! k: }5 s/ [0 S. j
' C# R0 u3 V# Y2 k7 O* g* k& p0 U
3 E- K9 N( N( l' I A& U2 J6 U9 B4 e6 S+ e8 l8 G* f
责任编辑:
! i$ J' W. Q4 g$ @' o' s# A, X2 J* S
5 X: i7 W! b' {0 j0 q
$ f) ^7 R4 u$ |1 @9 q. F% u
% F- `4 y" p8 k% [( Y/ G" } | 

