1.一质点作直线运动,某时刻的瞬时速度2/v m s =,瞬时加速度22/a m s =-,则1秒后质点的速度( D )
1 {. R4 x# x2 k5 P' [(A)等于零 (B)等于2/m s - (C)等于2/m s (D)不能确定. B x9 P$ z( A0 E. S& I9 V
2.一质点沿半径为R 的圆周做匀速率运动,每t 时间转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为( B ) (A)0 m2 y, B) k! I
2R t π,2R t π (B)O, 2R t π (C)0,0 (D)2R
$ Q H* c3 \+ V. j" m# Ct8 G1 V2 z% L! j- _% c
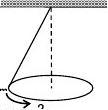
π,0 3.如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动。设该人以匀速率0v 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( c )6 H: d6 `7 R3 X- h: E* E3 w
(A)匀加速运动,0" G0 s* G0 C( L- ?% B
cos v v θ=# k# ?( T5 s1 _
(B)匀减速运动,0cos v v θ= (C)变加速运动,0cos v: I }9 y- m% D6 H
v θ+ e# m0 t# \6 b& ?& i& S
= (D)变减速运动,0cos v v θ=" C7 a3 y% p" Q% W' @! s
(E)匀速直线运动,0v v =' ]3 e, ?# F$ V& |- d b) }) F
4. 以下五种运动形式中,a ?9 E% M: a+ m+ v; C0 x
保持不变的运动是( D ) (A) 单摆的运动. (B) 匀速率圆周运动. (C) 行星的椭圆轨道运动. (D) 抛体运动. (E) 圆锥摆运动.9 ^# N8 o/ S" E3 M( O
5. 质点沿轨道AB 作曲线运动,速率逐渐减小,图中哪一种情况正确地表示了质点在C 处的加速度 ( C )) }4 G; O8 o: G: m: n3 T
( v) |, |& K2 N1 ~" d- D
3 P3 W& x0 X7 M/ t
* P+ J2 Z# w. [) t3 ]7 B5 C% u7 e1 \& s r. u
(A) (B) (C) (D4 k1 x& K8 ^+ |! F: I4 L
/ s+ d2 D, Q- o
1.一物体作如图所示的斜抛运动,测得在轨道P点处速度大小为v ,其方向与水平方向成30°角。则物体在P点的切向加速度a τ= ,轨道的曲率半径ρ= 2v2/√3g 。5 ?5 P. l0 G* ]
2. 轮船在水上以相对于水的速度1V r 航行,水流速度为2V r ,一人相对于甲板以速度3V r) ~. q v: O* e6 s2 X2 ~5 P
行走,如人相对于岸静止,则1V r 、2V r 和3V r$ t: J7 S# u) T# d4 p) ^- b! Y
的关系是:v1+v2+v3=0____。8 q8 J9 R7 ?$ P/ T* D+ o, r
3.加速度矢量可分解为法向加速度和切向加速度两个分量,对匀速圆周运动,_切_向加速度为零,总的加速度等于_法向加速度。
% m5 m5 c3 m6 C: g5 H; _) @ ) k; |4 J& {0 D6 t. Z9 J0 ^
1.如图所示,一汽车在雨中沿直线行驶,其速度为v 1,下落雨的速度方向与铅直方向的夹角为θ,偏向于汽车前进方向,速度为v 2.今在车后放一长方形物体,问车速v 1为多大时此物体刚好不会被雨水淋.! U9 { T3 [8 P/ O" X4 G% D
解:雨对地的速度等于雨对车的速度加车对地的速度,由此可作矢量三角形.根据题意得tan α = l/h .5 E" l% {6 t0 [& h9 D2 R/ r
根据直角三角形得v 1 = v 2sin θ + v 3sin α,9 S: ^6 ]6 ?+ `
其中v 3 = v ⊥/cos α,而v ⊥ = v 2cos θ,
: P. S5 K0 v3 }% _, C) w0 d因此v 1 = v 2sin θ + v 2cos θsin α/cos α, 即 .
; Q+ N$ N2 t; q. Z( x- m2.质点沿半径为R 的圆周按s =2
" n+ \. @3 u9 P' R. F029 G) u2 B4 h* W
1bt t v -# g+ x8 H* Z) t& K( o5 H* K
的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点加速度的大小;(2)t 为何值时,加速度在数值上等于b . 解:(1)bt v t s% G5 ~9 ^' o6 I: t+ D8 A" z" O% J7 D* d2 ~
v -==
( G8 M4 G( p9 r! r& M0d d b t% U4 v# b! @' b A
v a -==d d τ
6 e2 }' w, @" f2 RR
) D3 i& w7 L% o( mbt v R v a n 2" g% z5 R Y4 w
02)(-==
, a: h# E6 k+ ~% J0 E2 T$ o则 2& p9 |8 j1 J7 y/ n
4
5 N# \% v0 c8 q* G' a02
% T; x6 P7 r, m+ R7 [7 a3 g& B9 t228 w: {( D0 _; x8 `
)(R
7 C% x- R d! ?0 f: |bt v b a a a n
# Y# C: g) }2 L, N7 p-+=+=τ (2)由题意应有 2 Y$ u5 T: O1 k. {) {/ }
4
- ]5 U* v6 P' _! W% v; h9 L02
- L& W( @2 A: L. p% ?0 ]' K$ f1 l# x)(R bt v b b a -+==) j1 g/ }9 y! F
即 0)(,)(402. q4 B5 k& x% u0 q8 F
41 M {4 j o3 ?' T
02
" r8 v/ s0 J2 g1 N& g2
# O" T" I u" N3 u=-?-+=bt v R" ~! T$ f* [+ H6 q ^( H: U; F
bt v b b ∴当b
; |& I" S# r& s9 Av t 0
4 t5 o! i& }6 E=
' @2 `6 B& @% f' A5 }( t时,b a = 二章
, G+ c1 ?% S1 t. `4 `1.一个质量为m 的物体以初速度0v 从地面斜向上抛出,抛射角为θ,若不计空气阻力,当物体落地时,其动量增量的大小和方向为( c )
( a( o: L, ?. W x9 N# w(A)增量为0, (B)θsin 20mv ,竖直向上; (C)θsin 20mv ,竖直向下; (D)θcos 20mv ,水平;
- \- i1 M/ v6 v! M: F9 s% U2. 质点的质量为m ,置于光滑球面的顶点A 处(球面固定不动),如图所示.当它由静止开始下滑到球面上B 点时,它的加速度的大小为( d )- |4 X9 I5 i- t, v) n; o' F
(A))cos 1(2θ-=g a (B)θsin g a = (C)g a = (D)θθ2222sin )cos 1(4g g a +-=.
- V/ c0 Q$ H5 h8 n- X- G* q* v) a
: e: K$ a0 q. Y* m# ^9 ~3.有两个倾角不同,高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则(d ) (A)物块到达斜面底端时的动量相 (B)物块到达斜面底端时的动能相等 (C)物块和斜面(以及地球)组成的系统,机械能不守恒 (D)物块和斜面组成的系统水平方向上动量守恒.
& }& g- r+ Z j9 }3 G2 G& s4. 一炮弹由于特殊原因在水平飞行过程中,突然炸裂成两块,其中一块作自由下落,则另一块着地点(飞行过程中阻力不计) ( a )9 s' ^4 r) A/ P/ `, V1 ~" c
(A) 比原来更远 (B) 比原来更近 (C) 仍和原来一样远 (D) 条件不足,不能判定.
- t, A5 z& W) ]& g3 ?) j5. 水平公路转弯处的轨道半径为R ,汽车轮胎与路面间的摩擦系数为μ,要使汽车在转弯处不致于发生侧向打滑,汽车在该处行驶速率( b ) (A)不得小于Rg μ (B)不得大于Rg μ* \! V6 |. S# ^+ x( D( f {
(C)必须等于Rg μ (D)应由汽车质量决定
' j$ w- X% i2 i' O5 U' s 0 P3 x N- H3 Q3 V" g& l
1. 如图所示,竖直放置的轻弹簧的倔强系数为k ,一质量为m 的物体从离弹簧h 高处自由$ i/ f5 T X6 @' `, ]2 M
下落,则物体的最大动能为k$ u" c+ c+ l8 |
g m mgh 22
# |3 ?, d) H# a, H2+。" K$ r3 P9 p% L5 f
$ B4 ]5 ?8 ^/ {+ J' V- [( t
2.一质量为2kg 的物体沿X 轴运动,初速度为50m/s ,若受到反方向大小为10N 的阻力的作用,则产生的加速度为__-5_______m/s 27 N3 a4 R2 i( y$ P# ^# P W
,在该阻力的作用下,经过 5 s物体的速度减小为初速度的一半。
V3 x% o& c" c$ v, {$ P3.在光滑的水平面内有两个物体A 和B ,已知2A B m m =。(a)物体A 以一定的动能k E 与静止的物体B 发生完全弹性碰撞,则碰撞后两物体的总动能为_k E ; (b)物体A 以一定的动能k E 与静止的物体B 发生完全非弹性碰撞,则碰撞后两物体的总动能为_2
2 L4 x% X% x. g3 u4 n9 N3/ ^$ S# W, ~) R; i
k E ___。
, ` g1 `' \" s9 e 1.如图所示,光滑水平桌面上,一根轻弹簧(弹簧的倔强系数为k )两端各连着质量为m 的滑块A 和B 。如果滑块A 被水平飞来的质量为m/4、速度为v 的子弹射中,并留在其中,试求运动过程中弹簧的最大压缩量。
, e+ G9 E' `, ]3 i. i5 T& M9 \$ j0 u4 ~; q ~& K- N) J
解: 子弹进入物块A 的过程中,子弹、物块A 在水平方向上动量守恒9 M. {4 P7 M, Q! v
* B/ G4 Z8 J/ \# J
1# ~/ O5 i: ~* h* f5 i3 ~: ^3 l
154415" K2 y+ e5 \) H" W! ?
mv mv v v' a6 p+ O" m/ @+ ^ U( Z: e
==( i- N1 q( p: e' @
以子弹、物块A 、B 为系统,弹簧具有最大压缩量时,子弹、物块A 、B 具有相同的速度'v ,系统在水平方向上动量守恒,% M2 y/ l. {' m1 K$ {
$ X, x3 X3 W6 V7 A4 S4 X', f5 P- q. k4 o* b" I( L- n
'94419! H7 [& `+ e* n6 |& F5 e
mv mv v v5 p7 V9 A6 a, e& l4 L8 P
== 系统达到相同速度的过程中,有机械能守恒:
) `4 h# ]4 {+ h. [22'2
: |! U) r% r/ B: D+ f4 `1max 1511924224
, R% L; G, |1 `7 N' I: Lm m v kx v =+6 h- H; x& c5 x1 D4 j# P
max x =
( _; ^' w" n; v' S9 } a
8 i8 E" n& p4 p6 Y) O5 Z2. 一质量为M 的平顶小车,在光滑的水平轨道上以速度v 做直线运动。今在车顶前缘放上3 x. U1 B- o! ]6 d0 L. h% E$ d3 C
一质量为m 的物体,物体相对于地面的初速度为0.设物体与车顶之间的摩擦系数为μ,为使物体不致从车顶上跌下去,问车顶的长度l 最短应为多少7 u/ v' b* a9 I% H, W0 r
解:由于摩擦力做功的结果,最后使得物体与小车具有相同的速度,这时物体相对小车
8 P8 i0 ?! v7 j静止而不会跌下。以物体和小车为一系统,水平方向动量守恒,有6 J! D. v( I% B% `- v. o, t
V m M Mv )(+=1 ?# ~' I( z% ^/ I- U9 h2 ?
一对摩擦力的功为:222
# D* W8 n# |2 W* i) L' s7 ~+ Z* K3 d( ]1
% G3 g, p) U+ x! W+ B" H. y1 r)(21Mv V m M mgl -+=
/ a. y$ j! }* D$ \-μ 联立以上两式可解得车顶的最小长度为:)6 t0 j$ n, S* A o
(22
0 i7 |2 t( W( Z, f2 c& Y( S7 Vm M g Mv l +=μ
( a+ r. j \) ^1 z0 d+ `+ |34.一质量为m 的物体,从质量为M 的圆弧形槽顶端由静止滑下,设圆弧形槽的半径为R ,张角为/2π,如图所示,所有摩擦都忽略,求:(1)物体刚离开槽底端时,物体和槽的速度各是多少(2)在物体从A 滑到B 的过程中,物体对槽所做的功W 。 解:(1)物体运动到槽底时,根据机械能定律守恒得8 y1 N$ r: K) M, `
/ p# u, G# N1 Z- d1 s; j- xA B7 y) b0 s( P+ Z9 L( t
,
4 V# u% s7 m5 k1 e根据动量守恒定律得 0 = mv - MV . 因此,
2 I' A/ y9 P: t E解得, 从而解得.5 p) M% d r% E% Y) _
(2)物体对槽所做的功等于槽的动能的增量 .
7 c' o3 s- e) z- {* k4.一质量为kg m 2=的质点在合力为:)(23)(N j t i t F ρ
3 q: r$ T4 R6 q8 n: y: W! Cρρ-=的作用下在xoy 平面内运动,
7 H9 P6 j3 `4 O, H, O; Y)(0s t =时质点的初速为:)(0s# ` t% g7 ^/ i `9 M
m" X$ _; i" q1 z. l- E
j i v ρρρ-=。试求:: @3 ?* L) q: M" f! ?
(1)t = 2(s) 时质点的速度;(2)t = 0(s) 至t = 2(s)时间内合力对质点冲量; (3)t = 0(s) 至t = 2(s) 时间内合力对质点所作的功。 解: (1))(34)2(s
2 @0 s2 W! U4 |8 `' Z7 Jm j i t v ρ2 A h) O5 h. J& O0 C
ρρ
' ^) g6 X1 x7 m( o1 _5 h-==
0 m7 b' }) A+ ~3 ? Q6 s(2))(46)(0
! i$ ]4 E- b1 r) J) f: E7 K) j! Is N j i dt t F I t t ?-==?1 K* R' R3 p, U' o
ρ
' ~# U+ Q O$ }1 \/ Z+ ?7 ?ρρρ
! m0 A# G/ [3 m6 n" o& E$ n: `(3)23k A E J =?=
1 p! |! B. c/ o3 h=30+4t (式中F x 的单位为N ,t 的单位为s)的合外力作用在质量m=10kg 的物体上,试求(1)在开始2s 内此力的冲量I ;(2)若物体的初速度V 1=,方向与F x 相同,在t=2s 时,此物体的速度V 2。 解: (1) 2.0
^' n# I) W) [8 G R. c$ A! |9 X2.0 2.020: S! A& C4 T9 l$ d4 a- n2 ?8 y
$ E% i, _+ A! b4 r(304)(230)
( e: {$ p3 F$ f5 L68I Fdt t dt t t N s =5 ]) y. ]* L) D2 |' \: ?1 u
=+=+=?! r% H5 L, {; j. ^
?g
( p! J2 M( k8 Z$ u$ W(2)由质点的动量定理:0I p mv =?=-v v v
' G( n [7 d& t/ x1 W) S- c / j2 J# c+ X5 E6 h
18/v m s = 三章
8 ? T$ }9 A$ y1. 关于力矩有以下几种说法,在下述说法中正确的有:( B )①对某个定轴而言,内力矩不会改变刚体的角动量;②作用力和反作用力对同一轴的力矩之和必为零;③质量相等,形状和大小不同的两个刚体,在相同力矩作用下,它们的角加速度一定相等。 (A)只有②是正确的 (B)①、②是正确的 (C)②、③是正确的; (D)①、②、③都是正确的.
" V5 G, Q6 H, w8 H2.关于力矩有以下几种说法,其中正确的是( B ) : (A)内力矩会改变刚体对某个定轴的角动量(动量矩);5 w& }2 \/ m' s- f( r8 s: G
(B)作用力和反作用力对同一轴的力矩之和必为零; (C)角速度的方向一定与外力矩的方向相同;7 \4 V, x% |: P& e: N
(D)质量相等、形状和大小不同的两个刚体,在相同力矩的作用下,它们的角加速度一定相等。
9 Y2 B6 o1 e4 }: e3.一个转动惯量为J 的圆盘绕一固定轴转动,初角速度为0ω。设它所受阻力矩与转动角速度成正比M=ωk -(k 为正常数),它的角速度从0ω变为0ω/2所需时间是( Jln2/k ) (A) J /2 (B) J /k (C) (J /k )ln 2 (D) J /2k 。% h' s. u/ p% {1 V
4.一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。现有一质量为m 的子弹以水平速度v 0射向棒的中心,并以v 0/2的水 平速度穿出棒,此后棒的最大偏转角恰为?90,则v 0的大小为( A ) (A)# O- B& q2 t, \3 r) y, u; @
3/4gl m: T7 Z. M# u/ {4 O
M (B) 2/gl (C)# C* X/ u7 n6 n$ D1 S0 J
gl m
4 F+ x1 t# I# z7 _M 2% T! K B8 L7 m* V
2 j5 `3 W! a0 v% L( ^9 A/ x8 C; u- V
5.( )如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统 C" M0 Q G; I7 `. L
- [; J, `: a; G4 u' W4 Y |6 z(A) 只有机械能守恒 (B) 只有动量守恒 (C) 只有对转轴O 的角动量守恒 (D) 机械能、动量和角动量均守恒.6 r: }; r" t v8 x2 F
1. 图示为一圆锥摆,质量为m 的小球在水平面内以角速度?- e2 e/ n* Z; R: n3 \
 " E1 Q: F$ M, Z7 `8 N) f+ y9 p$ Y, Q4 ?
登录/注册后可看大图 " E1 Q: F$ M, Z7 `8 N) f+ y9 p$ Y, Q4 ?
登录/注册后可看大图
匀速转动,在小球转动一周的过程中 (1)小球动量增量的大小等于___0___; (2)小球所受重力的冲量的大小为__2∏mg/w _; (3)小球所受绳子拉力的水平分量冲量大小为_2Πmg/w _。
$ a) J6 r; ]) ], R5 D( ]0 ?2.如图所示,一匀质木球系在一细绳下端(不计细绳质量),且可绕水平光滑固定轴O 转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则此击中过程中木球、子弹系统对O 点的角动量__守恒 ,原因是_对O 点的合外力矩为0_。木球被击中后棒和球升高的过程中,对子弹、木球、细棒、地球系统的机械能_守恒___。
" h% |: P1 _ o* o; U7 Q } 6 z% w. B/ S2 a# W
1. 一质量为M =15 kg 、半径为R = m 的圆柱体,可绕与其几何轴重合的水平固定轴转动(转8 U6 t! C6 z+ D" F, w9 |
动惯量J =
$ y M5 t( V, O7 W4 q2 G22% G% r5 b$ U! [- k3 V, ~6 G
1
^6 G! k2 S3 x4 v" R( ^9 {# bMR ).现以一不能伸长的轻绳绕于柱面,而在绳的下端悬一质量m = kg
* E0 M4 f) T A- W 的物体.不计圆柱体与轴之间的摩擦,求:物体自静止下落, 5s 内下降的距离和绳中的张力. 解: J =
1 D9 P! H- ?/ r( P22
( V5 u4 T1 ~! W- ^1
4 |; l/ `4 h6 }& S0 Z. HMR = k g·m 2 ∵ mg -T =ma TR =J β a =R β3 p2 E3 S( _1 {3 p+ U
∴ a =mgR 2! r) {0 f6 t8 n, O7 R q
/ (mR 2% Q/ B" m6 B6 D2 W
+ J )= m / s 2) `- W- `$ N7 ^) Y% b1 {" O
下落距离 h =# x+ i& M+ u; E/ e4 m N
2 x0 d! J( J t' P2 W
2) y' |; d2 K7 ^9 g+ f
1at = m 张力 T =m (g -a )= N7 r$ S4 ]3 L# x& Y& I
2. 长为L ,质量为M (未知)的匀质细杆,一端悬于O 点,自由下垂,紧挨O 点悬挂一单摆,轻质摆线的长度也是L ,摆球的质量为m 。单摆从水平位置由静止开始自由下摆,与细杆作完全弹性碰撞。碰撞后,单摆正好停止。若不计轴承的摩擦,试求:(1)细杆的质量
* A6 _; Z8 p& r Q/ D0 S; ^?=M ;
& n# k8 R) b: `- J4 s8 Z! o(2)细杆被碰后,摆动的最大角度m ax θ。(设细杆绕O 点的转动惯量为 23. o% g: d% {# F/ w, p( F, L
1
3 F4 o' |- e* m6 B+ SML J =) 解:摆球与细杆作完全弹性碰撞,在碰撞过程中对0点的角动量守恒,且机械能守恒。
+ Q( B; H3 O* O8 S0 A! |8 f# T21
5 y% U% z% U, Z* p3ML ω=) m6 @+ e5 l8 i; d$ \8 T9 s% \
1 f! m( u6 I2 {* M# A j. `2211232 P& e1 {3 h0 s& v; \) p* x3 p
mgL ML ω=
& R3 A7 k* J: V1 Omax (1cos )2
3 b6 v$ L0 l* R& h$ [7 tL1 ^! _/ P$ t% L# N
mgL Mg θ=-
# C; Y5 U Z! k0 Y! t' p3 l解得:m M 3=;* {4 h" _: }) w; {. C$ X* K% x
70.53)3, B) V2 N5 v# n R0 O! ?
1
4 N. V6 V' r1 K& t. U4 p2 C(01max ==-Cos θ* E0 {. |+ ^' G7 {- |4 L+ H
" F5 K7 P' N+ D, u3 w9 E$ o9 R
四章
3 a. p3 h5 |! T, K z. T- Z1.( )一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的(D) (A)1/4. (B)1/
: ], D2 Q w4 x0 N2. (C)2/1. (D)34
: e. _. k" L; s# P2 r
" ]3 m+ A q# e# W) V% g2.( )两个同方向,同频率,振幅均为A 的简谐振动,合成后的振幅仍为A ,则这两个分振动的位相差为(A) (A)
+ |7 U2 W6 X, A, y2 h( y' |4 W" T1 K3π (B)2# w6 j$ ^6 A. {6 I ~) X
π (C)23π (D)π8 q5 D, {) j' O$ m5 i1 _. t* `! n& z
3. ( C )对一个作简谐振动的物体,下面说法正确的是
) U" P6 n( e. U (A)物体处在运动正方向的端点时,速度和加速度都达到最大值; (B)物体位于平衡位置且向负方向运动时,速度和加速度都为零; (C)物体位于平衡位置且向正方向运动时,速度最大,加速度为零; (D)物体处在负方向的端点时,速度最大,加速度为零。+ K2 w) q$ t* y7 u9 b7 j9 G
4.( A )在简谐波传播过程中,沿传播方向相距为λ2
& P! d+ ]6 z" F4 r# z1(λ为波长)的两点的振动速度必定+ {* r. ^6 A2 y0 h' v- b
(A)大小相同,而方向相反. (B)大小和方向均相同. (C)大小不同,方向相同. (D)大小不同,而方向相反. 5.( )平面简谐波在传播的过程,以下说法正确的是
: P) t" s9 z& m(A)质元离开平衡位置的位移y 为最大时,质元的势能最大,动能为零; (B)质元在平衡位置时动能最大,势能为零; (C)质元的机械能守恒; (D)质元在平衡位置时相对形变量
* m2 a3 O1 y# J8 s4 ]; Ly
9 ] y! h, q1 E' m |x) J* |3 F- c! A5 S+ m
??最大,其势能和动能都达最大值。 6. ( A )某时刻驻波波形曲线如图所示,则a ,b 两点相位差是 (A)π (B)2π (C)54
7 J+ E6 c+ ?6 ?, Mπ (D)0
" `/ p5 X6 y* C) v( U7.( D )机械波在弹性媒质中传播时,若媒质质元刚好经过平衡位置,则它的能量为: (A)动能最大,势能也最大 (B)动能最小,势能也最小 (C)动能最大,势能最小 (D)动能最小,势能最大." m9 D6 s) V/ i% W, V" s" x( U8 E
1.两个同方向不同频率简谐振动合成时,振幅随时间作周期性的缓慢变化,形成了振幅时而加强时而减弱的现象,该现象成为__拍__现象。
2 i t7 m/ X* W$ L) u& Y; `/ `2.一平面简谐波的波动方程为y=(400πt-20πx),式中各物理量的单位均为国际单位制(SI)。该平面简谐波的波速为 m/s 、波源振动频率为 Hz 。- S: J" H2 I: b
3.已知质点作简谐运动,其x t -如图所示,则其振动方程为 。
2 v) i. f! v, O6 H' p( z+ |1.一平面简谐波沿x 轴负向传播,波长 1.0m λ=,原点处质点的振动频率为/ t- e% S P+ P
2.0Hz υ=," e! N2 x- e `# ^; R6 r
振幅0.1A m =,且在0t =时恰好通过平衡位置向y 轴负向运动,求此平面波的波动方程.
3 I2 c+ N, k/ q% i: L# \. F' N
3 Z& q4 @! I1 r, N% T: V解: 由题知0=t 时原点处质点的振动状态为0,000 |


